Une proposition de corrigé du Brevet Pondichéry 2014 sous un format interactif avec des rappels de cours pour optimiser les révisions de vos élèves qui ne l’ont pas encore passé (les épreuves de métropole ont lieu plus tard, en juin, comme vous le savez sans doute !)
L’auteur, Stéphane Guyon, professeur de mathématiques au collège, présente ainsi son activité : « L’activité propose de s’entraîner avec le sujet de Brevet Pondichéry 2014 (c’est une épreuve anticipée du DNB pour les élèves de cette ville indienne). Le sujet est à imprimer en PDF. Les six exercices sont sous un format interactif pour s’entraîner en vue du DNB 2014 en juin 2014. »
Ancrage au programme scolaire
- Niveau : Troisième – Brevet 2014
- Discipline : Maths
- Thème : Annale et corrigé brevet Pondichery 2014
Exercice 1
Emma et Arthur ont acheté pour leur mariage 3003 dragées au chocolat et 3731 dragées aux amandes.
Arthur propose de répartir ses dragées de façons identiques dans 20 corbeilles, chaque corbeille doit avoir la même composition.
1) Combien lui reste-t-il de dragées non utilisées ?
2) Emma et Arthur changent d’avis et décident de proposer des petits ballotins dont la composition est identique. Ils souhaitent qu’il ne leur reste pas de dragées.
a) Emma propose d’en faire 90. Cela convient-il ? Justifier.
b) Ils se mettent d’accord pour faire un maximum de ballotins. Combien en feront-ils et quelle sera leur composition ?
Exercice 2
Cet exercice est un questionnaire à choix multiple (QCM).
Pour chaque ligne du tableau, trois réponses sont proposées, mais une seule est exacte.
Toute réponse exacte vaut 1 point.
Toute réponse inexacte ou toute absence de réponse n’enlève pas de point.
Exercice 3
« Je prends un nombre entier. Je lui ajoute 3 et je multiplie le résultat par 7. J’ajoute le triple du nombre de départ au résultat et j’enlève 21. J’obtiens toujours un multiple de 10. «
Est-ce vrai ? Justifier
Exercice 4
Une commune souhaite aménager des parcours de santé sur son territoire. On fait deux propositions au conseil municipal, schématisés ci-dessous :
• Le parcours ACDA
• Le parcours AEFA
Peux-tu les aider à choisir le parcours ? Justifie.
Exercice 5
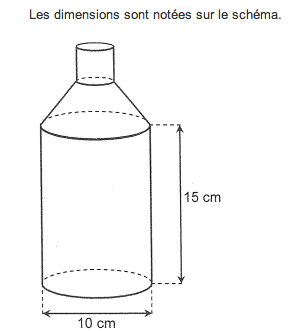
Voici une bouteille constituée d’un cylindre et d’un tronc de cône surmonté par un goulot cylindrique. La bouteille est pleine lorsqu’eIIe est remplie jusqu’au goulot. Les dimensions sont notées sur le schéma. Parmi les quatre graphiques cl-dessous, l’un d’entre eux représente Le volume V(h) de la bouteille en fonction de la hauteur h de remplissage du bidon.
Exercice 6
Le classement des médailles d’or reçues par les pays participant aux jeux olympiques pour le cyclisme masculin (Source : Wikipedia).
Télécharger le sujet complet sous format PDF en cliquant ici.
Activité pédagogique en Maths : Sujet et corrigé Brevet Pondichery 2014
Jouer l’activité en pleine page
Vous souhaitez réutiliser cette activité avec vos élèves ?
Pour reprendre l'activité :
https://www.education-et-numerique.fr/0.3/activity/embed.html?id=5360aa023361eb112e6fb35c
Utiliser le code iframe pour l’intégrer dans votre blog ou site pédagogique :
<iframe src='//www.education-et-numerique.fr/0.3/activity/embed.html?id=5360aa023361eb112e6fb35c' style='width: 600px; max-width: 1000px; height: 800px;' ></iframe>
Importer cette activité dans votre ENT ? par mail par mail, nous vous enverrons le package scorm nécessaire à l’intégration dans un ENT !
Vous souhaitez créer vos propres activités E&N ? N’hésitez pas, rejoignez l’environnement auteur en vous connectant ou en vous inscrivant. C’est rapide et vraiment facile !
A votre écoute :
Des remarques, des questions sur cette activité ? N’hésitez pas à laisser un commentaire 🙂

 Facebook
Facebook Twitter
Twitter



16 Commentaires
Séverine
Bonsoir,
il me semble qu’il y a une erreur dans la troisième partie de l’exercice 5. Le premier graphique est correct contrairement au graphique n°4. En effet, lorsque h=0, le volume est égal à 0. De plus, lorsque h=15, le volume du cylindre est d’environ 1178 cm3.
Marièke Poulat
C’est corrigé ! Merci pour votre remarque 😉
hugo
je crois que dans l’exo 6 partie 3 la réponse 37 correspond aux nombres de pays médaillé au moins une fois en or
Marièke Poulat
Effectivement, je vous laisse jeter un coup d’oeil à la réponse de l’auteur 🙂
pierrel
Bonjour,
Il me semble qu’il y a une erreur dans la 3ème partie de l’exercice 6.
70 % des pays médaillés ont obtenu au moins une médaille d’or.
Donc on calcule le nb de pays médaillés : 26/0.7 = 37
On en déduit le nb de pays qui n’ont obtenu que des médailles d’argent ou de bronze (c’est à dire le nb de pays médaillés – nb de pays ayant obtenu au moins une médaille d’or) : 37-26 = 11
Marièke Poulat
Réponse de Stéphane Guyon, l’auteur :
C’est une très bonne remarque. Une lecture trop rapide de l’énoncé m’a fait répondre à une autre question (sous-jacente et intuitive) mais pas à celle demandée. C’est corrigé 😉
Héloïse Taffus
Je ne comprends pas l’exercice 4: comment peut-on savoir lequel des deux parcours proposés est le mieux si l’on ne sait pas les critères de sélection ? Quel est le parcours idéal pour le conseil municipal ?
Pour la question « le parcours choisi par le conseil municipal sera… », après avoir répondu (au hasard) ACD, la correction m’indique que c’est faux car « 3,94 est plus proche de 4 que 4,2 ». Je suis d’accord avec cela, mais comment pouvais-je savoir qu’il fallait le périmètre le plus proche de 4 ?
Sinon je trouve ces exercices bien construits et la correction (et les aides) utiles et compréhensibles.
Marièke Poulat
Réponse de Stéphane Guyon, l’auteur :
Il y a eu un bug dans l’énoncé en bidouillant les figures… Une consigne a sauté au passage dans l’énoncé : « Ils souhaitent faire un parcours dont la longueur se rapproche le plus de 4 Km. » C’est rectifié.
emma
Je ne comprends pas les réponses de l’exercice 2. Elles me semblent erronées. Serait-il possible de les vérifier s’il vous plaît ?
Marièke Poulat
Réponse de Stéphane Guyon, l’auteur :
Les réponses sont justes avec des explications en ligne. Il s’agit d’un QCM, avec 5 questions sans aucun lien entre-elles, sur des chapitres très différents. Il faudrait préciser la ou les questions concernées pour mieux comprendre votre problème…
Camille
Je pense qu’il y a une erreur à la 4° question de l’exercice 4, on ne cherche plus le périmètre du triangle ACD mais celui du traingle AEF !
Bobby
Heu… A l’exercice 1, c’est quoi les réponses ?
Marièke Poulat
Il est vrai que le texte à trou ne permet pas encore de donner les réponses en cas d’échec…
Les réponses de l’exercice 1 (à ne regarder que lorsque vous l’avez fait, bien entendu !) sont :
> Page 1 :
On effectue les divisions euclidiennes du nombre de dragées par 20 soit :
150 + 3
et 186 + 11
Avec les dragées au chocolat, il fera donc 150 paquets de 20 et il lui en restera 3.
Avec les dragées aux amandes, il fera donc 186 paquets de 20 et il lui en restera 11.
Au total, il lui restera 14 dragées.
> Page 2 :
On cherche à savoir si 90 est un diviseur commun de 3003 et de 3731.
On observe que 33 + 33
Donc 90 n’est pas un diviseur de 3003.
On peut donc conclure que cela ne convient pas.
> Page 3 :
Le nombre de ballotins est un diviseur de 3003 et 3731.
Pour trouver le nombre maximum de ballotins, il faut donc trouver le PGCD de 3003 et 3731.
Pour le trouver, on applique l’algorithme d’Euclide :
1 + 728
3003 = 4 + 91
728 = 91 8 + 0
donc PGCD (3003;3731) = 91
Conclusion : Emma et Arthur pourront élaborer au maximum 91 ballotins.
Marine
Bonjour, je ne comprends pas dans l’exercice 4, j’ai reçu a trouvé le périmètre du parcours AEFA mais pour le parcours ACDA comment on fait car vous dites que le triangle ACD est rectangle mais ce n’est pas stipulé ? En plus sans l’angle droit impossible de calculer DA meme avec la réciproque de pythagore car on ne connaît pas sa valeur , merci d’avance
NathanN
Bonjour, il y a une erreur dans le QCM de l’exercice 4, il y a 2 triangles, et on demande quelle formule il faut utiliser mais 2 fois pour le même triangle ACD, et pas pour l’autre.. alors la réponse corrigé ne fonctionne pas avec la question… Pour ACD il faut Pythagore, c’est pour AEF qu’il faut Thalès, Merci
Marièke Poulat
@Camille, @Marine et @NathanN : Vous avez bien sûr raison ! Il y avait une petite erreur dans l’énoncé. C’est désormais corrigé ! Désolés !